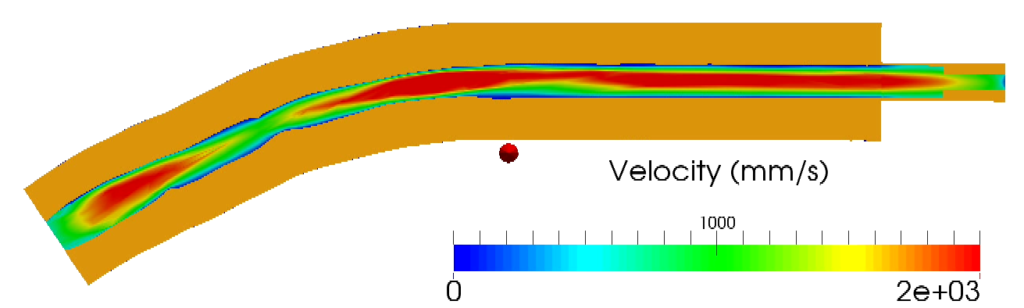
This is a fluid-structure interaction model (FSI) to simulate the blood flow and vessel wall mechanics of a mouse carotid artery. This FSI model is based on the immersed-body method (Yang, Xiang et al. 2016) which couples an open source finite element computational fluid dynamics (CFD) solver FLUIDITY and an in-house finite-discrete element solid solver SOLIDITY. The micro-CT scan projections were used to reconstruct the 3D geometry of the mouse carotid artery. The blood flow velocity measured by the ultrasound was used in the FSI model as the inlet boundary condition. Since the pressure measurement is difficult for the mouse carotid artery, an outlet boundary model (Pahlevan, Amlani et al. 2011) was used to model the compliance and resistance of the downstream vasculature. This simulation indicates the immersed-body FSI model has the potential to model blood flow and vessel wall mechanics for arteries.
In the simulation below, the wall deformations during pulsatile flow can be seen together with the FEMDEM mesh. The large strain formulation employed is vital for capturing typical bio-tissue behaviour.
To validate the two-way coupling model, the classical benchmark test of an unstable oscillating pressurised large strain elastic membrane coming to rest has been used, see below.
Finally, shown below is the remarkable two-way solid-fluid coupling capability applied to a brittle elastic cantilever beam undergoing bending and eventual fracture due to a pressure wave modelled with a compressible gas. This technology is to be applied to understand rupture of the fibrous cap of atherosclerotic coronary artery plaques.
References
Pahlevan, N. M., F. Amlani, M. H. Gorji, F. Hussain and M. Gharib (2011). “A physiologically relevant, simple outflow boundary model for truncated vasculature.” Annals of biomedical engineering 39(5): 1470-1481.
Yang, P., J. Xiang, F. Fang, D. Pavlidis, J.-P. Latham and C. C. Pain (2016). “Modelling of fluid–structure interaction with multiphase viscous flows using an immersed-body method.” Journal of Computational Physics 321: 571-592.