Background
Whereas at the scale of an intact rock core, the fracture style and strength outcome of a Brazilian disc or uniaxial compressive strength test is often quite predictable, fracture processes in rock are poorly understood when examined at the grain scale where properties are heterogeneous. Fracturing may exploit grain boundaries, weak minerals and pores. Many methods of rock cutting, rotary and percussive drilling, water jetting etc. apply very specific loading regimes in order to excavate chippings. To study fracturing mechanisms to make this more efficient, engineers are seeking to benefit from modelling methods. The creation of representative interlocking crystalline and porous rock microstructures is the starting point. Recent developments in the FEMDEM fracturing code Solidity (see SolidityProject.com) allow internal grain and grain boundary strengths to be accounted for and applied to examine rock breakage processes see Fig. 1.
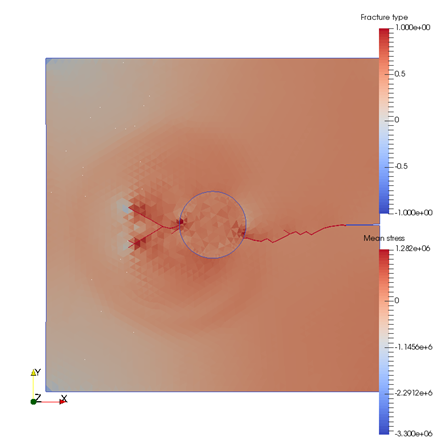
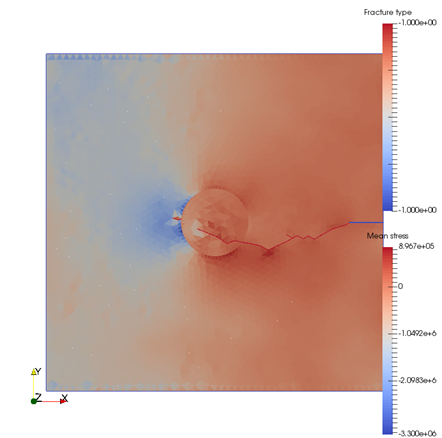
Fig. 1 Proof of concept grain boundary strength model recently implemented in Solidity by Kampitsis 2018. The tensile crack forced at the right boundary opening notch is modelled advancing and interacting with a harder circular inclusion (Left) and with a softer inclusion (Right).
With such an advanced fracture model that can model grain boundary fracturing and minerals with different elastic and strength properties, the remaining task is to create representative microstructure geometries and assign appropriate properties to the phases.
While interlocking mineral fabric geometries and mesh files can be created for simple eg metallic materials, eg using Voronoi tessellation methods, it is more challenging to represent porous rocks with grain and void fabrics typical of sandstones. Sandstone reservoir rocks are very common, yet fracture mechanisms at grain scale are poorly understood. This project will therefore focus on numerical development of porous rock microstructures and provide simple examples of breakage of such theoretical rock textures using sophisticated fracture models. Previous attempts to model microstructure effects for study of fracture path and rock failure mechanisms are shown in Gao et al 2016, Fig. 2.

Fig. 2 Left: Photo-micrograph of granite and Right: attempt to generate representative granite rock fabric as a basis for modelling fracture with micro-structure effects. Reported in Gao, F. et al. (2016) Numerical simulation of microstructure of brittle rock using a grain-breakable distinct element grain-based model, Computers and Geotechnics 78 203–217.
The approach being developed in Solidity is shown in Fig. 3. Such models are often only partially successful when fracture patters are compared with experiments. An ability to model porous micro-structures is shown in work on porous concrete in Fig. 4, however for that study fracture cannot go through the grain.
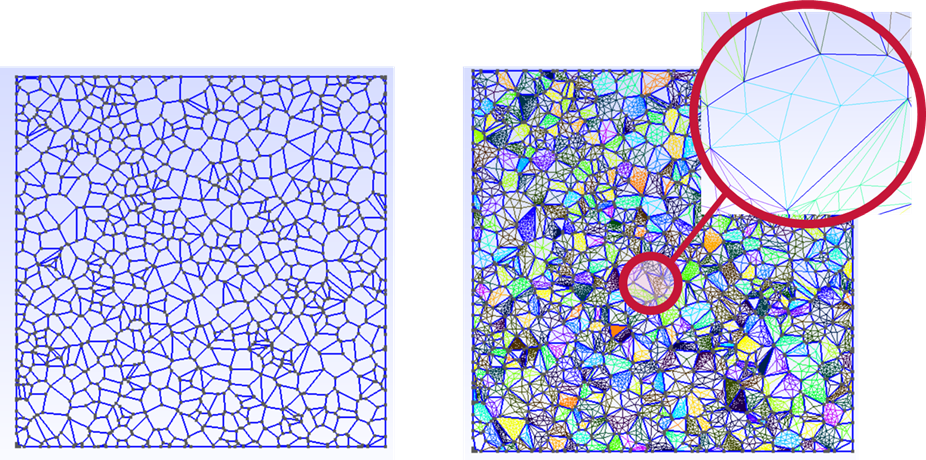
Fig. 3 Voronoi method for grain micro-structure (left) and meshing of grains (right). Further improvements in grain mesh generation are in development in order to apply the Solidity fracture models shown in Fig 1.
The project
You will begin with an introduction to a new microstructure generation code written in MATLAB, based on Voronoi methods. You will investigate ways of introducing controlled values of bulk porosity with a random population of pore ‘grains’ that are consistently smaller than the main clastic grains. Several other approaches will be considered for the project, these may include multi-point geostatistics, grain deposition process models and meshing tool options. A considerable volume of laboratory strength test data exists on sandstone specimens, from which the quality of the fracture modelling can be compared.

Fig. 4 Dynamic fracture modelling in a numerical model of concrete microstructure (a-f), varying aggregate-mortar mix ratios and structures, (g-j) increasing porosity in concrete structure; from Zou, W. et al., 2016. Mesoscopic simulation of the dynamic tensile behaviour of concrete based on a rate-dependent cohesive model. International Journal of Impact Engineering, 95 (2016) 165–175.
