Plasticity models have been developed for implementation in FEMDEM by Nikos Karantzoulis. Supervisors were John-Paul Latham, Jiansheng Xiang and Bassam Izzuddin.
Numerical solution of Governing Equations
The general continuous equations of elasto-plasticity are discretised by applying a fully implicit (backward) Euler scheme, which has been shown to be accurate and unconditionally stable.
The global incremental problem then becomes the following: at every timestep, for every discrete element, for every finite element, for every integration point, given a deformation gradient tensor and with current history of deformation known, solve the system of discretised governing equations. To do this, the classic algorithmic approach is followed, separating the stress space to admissible and inadmissible regimes and deploying return mapping strategies when necessary.
The four basic plasticity models (von Mises, Tresca, Mohr Coulomb, Drucker Prager) for perfect and hardening plasticity have been successfully implemented in Solidity within the FEMDEM framework.
Recently current implementation was extended to finite strain plasticity as well, expanding on existing small strain routines.
Verification Tests
Multiple benchmark test cases have been considered, verifying Solidity’s accuracy, stability and computational efficiency for dealing with both quasi-static and dynamic elasto-plastic problems. Some examples can be seen below.
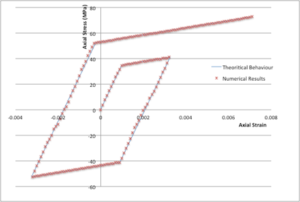
a) Uniaxial tests
Cyclic compressive/tensile loading is applied to cylindrical specimens while the stress path is captured. Resulted graphs show perfect match with the expected theoretical behaviour for both elastic-perfectly plastic and elastic-hardening plastic cases behaviour.
Deformed shape and stress-strain path of uniaxial loading/unloading of an elasto-plastic cylinder
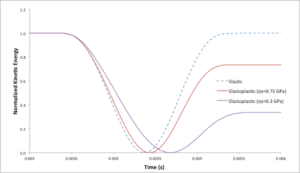
- b) Elasto-plastic collision of spheres
In high-speed collisions of spheres the driving energy dissipating mechanism is the plastic deformation that is occurring in the vicinity of the impact area of the bodies.
The collinear impact of two identical spheres with initially equal and opposite velocities is illustrated below, for both the cases of elastic and elasto-plastic impact. One can observe both the kinetic energy loss and resulted irreversible deformations due to the inelastic impact.
Solidity can handle any type of inelastic collision of objects with arbitrary shapes and velocity directions.
Time history of kinetic energy during elastic and elasto-plastic impact of spheres.
- c) Large-strain plasticity.
Animation below demonstrates the simulation of the normal impact of a copper rod against a flat rigid surface (Taylor bar test). The very rapid applied load (impact speed 227 m/s) and its characteristic deformed resulting shape have made this problem one of the most challenging benchmarks for dynamic large strain FEM codes. While in most cases appropriate boundary conditions are usually have to be applied, within the FEMDEM framework we can realistically simulate this class of problems as elasto-plastic impacts of discrete objects. This example also demonstrates how well Solidity deals with numerical issues usually arising in large incompressible plastic deformations (e.g. volumetric locking).
REFERENCES
Karantzoulis N, Xiang J, Izzuddin B and Latham JP, 2013, NUMERICAL IMPLEMENTATION OF PLASTICITY MATERIAL MODELS IN THE COMBINED FINITE-DISCRETE ELEMENT METHOD AND VERIFICATION TESTS, DEM6 – International Conference on DEMs, Pages: 319-323